Bayesian Probabilities
PRML Chapter 1.2.3 (Expectations and Covariences | Gaussian Distribution)
Định lý Bayes
Một trong những định lý quan trọng nhất của xác suất chính là định lý Bayes (tiếng anh là Bayes’ Theorem). Định lý được phát biểu như sau:
Định lý Bayes: Cho $X$ và $Y$ là 2 biến cố, khi đó xác suất có điều kiện $P(Y \mid X)$ là: \[ P(Y \mid X) = \dfrac{P(X \mid Y)P(Y)}{P(X)} \]
Giờ hãy nhìn thật kỹ vào công thức này, nhìn nó đơn giản thế nhưng chưa chắc đã vậy đâu. Trước khi bắt đầu giải thích sâu thì các bạn hãy đọc meme ở hình 1.
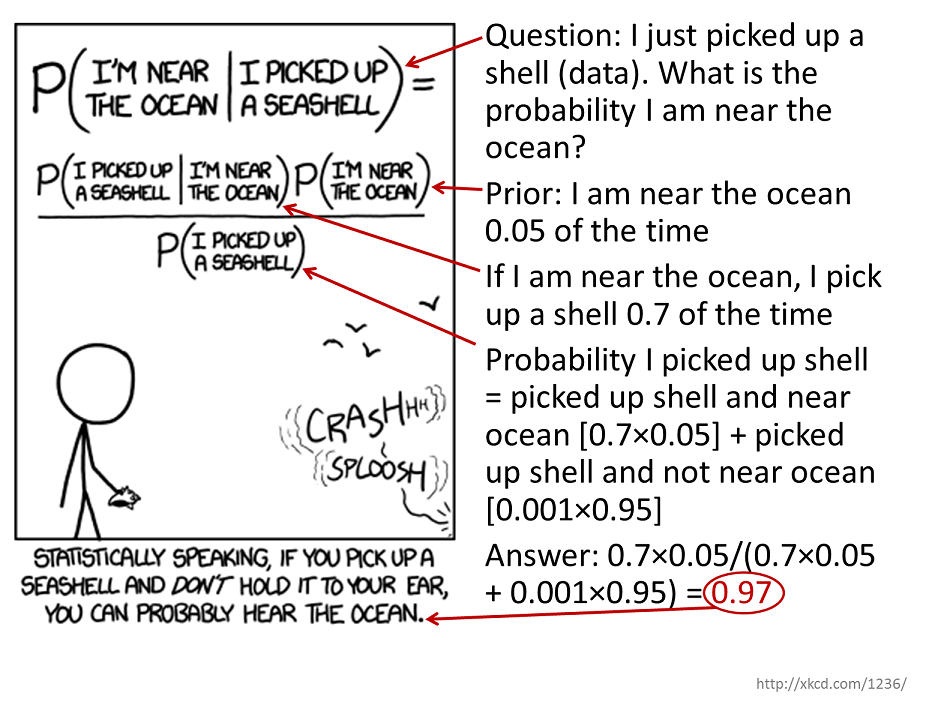
Ở hình 1, câu hỏi sẽ là “Giờ tui mới lụm được cái vỏ sò, xác suất mà tui ở gần biển là bao nhiêu ?”. Trước khi trả lời câu hỏi, thì mình biết được xác suất mình gần biển sẽ là $0.05$ (bởi vì mình lên mạng mình thấy vậy 💀). Giờ nếu mình ở gần biển (chắc ở biển luôn, gió thổi hù hù) thì xác suất mà mình lụm cái vỏ sò sẽ là $0.7$, thế nhưng giả sử mình không gần biển thì xác suất mình lụm được vỏ sò là $0.001$ (thấp là đúng 🥲, mình thêm vào bởi vì hình không có).
Giờ mình đặt $A$ là biến để mình biết ở gần biển hay không, $A = 1$ là gần và $A = 0$ là không. Tương tự, mình đặt $B$ là biến để mình biết mình có lụm vỏ không, $B = 0$ là mình không lụm vỏ sò và $B = 1$ là mình lụm vỏ sò. Khi này mình có:
\[\begin{aligned} P(A = 1) &= 0.05 \\ P(B = 1 \mid A = 1) &= 0.7 \\ P(B = 1 \mid A = 0) &= 0.001 \end{aligned}\]Nếu để ý, để trả lời câu hỏi, mình cần tìm xác suất $P(B = 1 \mid A = 1)$. Nếu áp dụng định lý Bayes, mình sẽ có:
\[P(A = 1 \mid B = 1) = \dfrac{P(B = 1 \mid A = 1)P(A = 1)}{P(B = 1)}\]Vậy mình chỉ còn thiếu xác suất $P(B = 1)$ thôi. Nếu áp dụng sum rule, ta có:
\[\begin{aligned} P(B = 1) &= P(B = 1, A = 0) + P(B = 1, A = 1) \\ &= P(B = 1 \mid A = 0)P(A = 0) + P(B = 1 \mid A = 1)P(A = 1) \\ &= 0.001 \cdot (1 - 0.05) + 0.7 \cdot 0.05 \\ &= 0.03595 \end{aligned}\]Giờ đã có đủ, áp dụng Bayes thôi:
\[\begin{aligned} P(A = 1 \mid B = 1) &= \dfrac{P(B = 1 \mid A = 1)P(A = 1)}{P(B = 1)} \\ &= \dfrac{0.7 \cdot 0.05}{0.03595} \\ &\approx 0.97 \end{aligned}\]Vậy là nếu mình nhặt được một vỏ sò thì có đến $97\%$ mình ở gần biển 😲, mặc dù xác suất mỗi cái nhìn rất ít, nhưng khi dùng Bayes lại cho xác suất rất cao.
Nhìn kỹ hơn định lý Bayes
Giờ nếu ta xem, xác suất về một biến cố nào đó chính là thông tin về biến cố đó. Ví dụ $P(\text{tối nay bạn đi ngủ}) = 0.7$ thì mình biết là tối nay, có $70\%$ khả năng là bạn sẽ đi ngủ và đây là thông tin mình có về việc bạn đi ngủ tối nay.
Nếu nhìn vào công thức Bayes, người ta có quy định về tên gọi của từng xác suất có mặt trong công thức đó. Đầu tiên là $P(Y)$ sẽ được gọi là prior probability (hay xác suất tiên nghiệm), sở dĩ gọi vậy là vì đây là thông tin đầu tiên mà ta có khi nói về biến cố $Y$. Thay vì hiểu $P(Y)$ là xác suất $Y$ sẽ xảy ra như cách thông thường, theo Bayes (hay trường phái Bayes, gọi là Bayesian) thì $P(Y)$ là degree of belief (hay mức độ niềm tin) mà ta tin rằng $Y$ sẽ xảy ra, $P(Y)$ càng cao thì ta càng tự tin vào suy nghĩ của mình hơn.
Thế nên theo Bayesian, xác suất mang tính chủ quan hơn, ví dụ bạn An ở Mỹ, nên bạn An chưa bao giờ ăn bún đậu mắm tôm do đó $P(\text{bún đậu ngon})$ của bạn An rất thấp, còn mình mỗi tuần ăn 1 lần nên $P(\text{bún đậu ngon})$ của mình rất cao (ngon thật). Cùng một biến cố nhưng lại có xác suất khác nhau, nhưng việc này do đâu nhỉ ?
Giờ giả sử, bạn An ăn bún đậu lần đầu, khi đó với thông tin mới bạn An có là $P(\text{đã ăn bún đậu})$, niềm tin của bạn An được gia tăng (hoặc giảm xuống) bởi vì $P(\text{bún đậu ngon})$ giờ đã trở thành $P(\text{bún đậu ngon} \mid \text{đã ăn bún đậu})$. Ta gọi cái này kiểu như update niềm tin của mình vậy, mình sẽ có một niềm tin ban đầu, khi nhìn thấy một cái gì đó mới, mình sẽ update cái niềm tin của mình và update bằng công thức Bayes. Vậy do mình đã ăn bún đậu rất nhiều lần nên $P(\text{bún đậu ngon})$ của mình cao là đương nhiên (mình đã update nhiều lần rồi, mỗi lần ăn ngon nên update nhé).
Hết ví dụ thì ta đã rõ hơn Bayesian chút rồi. Ta gọi $P(Y \mid X)$ là posterior probability (hay xác suất hậu nghiệm) bởi vì đây là niềm tin ta có sau khi quan sát được một thông tin mới xảy ra, ở đây là $P(X)$, ngoài ra $P(X)$ được gọi là evidence. Còn lại là $P(X \mid Y)$, xác suất này được ta gọi là likelihood, này thì khá khó giải thích (nhưng mà rất quan trọng đó) nên mình để các độc giả tự giải thích 😭.
Bayes trong Machine Learning
Định lý Bayes cũng có thể áp dụng trong Machine Leanring như sau. Giả sử rằng ta có tập dữ liệu $\mathcal{D}$ và một model có bộ tham số là $\mathbf{w}$. Mục đích của ta là với tập dữ liệu $\mathcal{D}$ như này, bộ tham số $\mathbf{w}$ của ta như nào mới là tốt, tức là tìm xác suất $p(\mathbf{w} \mid \mathcal{D})$.
Giả sử ta đã chọn được một mô hình với bộ tham số $\mathbf{w}$. Trước khi có tập dữ liệu $\mathcal{D}$, ta ngầm giả định rằng $\mathbf{w}$ có phân phối là $p(\mathbf{w})$. Sử dụng định lý Bayes, ta có:
\[p(\mathbf{w} \mid \mathcal{D}) = \frac{p(\mathcal{D} \mid \mathbf{w})p(\mathbf{w})}{p(\mathcal{D})}\]Phân phối $p(\mathcal{D} \mid \mathbf{w})$ ở bên phải của định lý Bayes là một hàm phụ thuộc vào $\mathcal{D}$, thế nhưng nếu ta xem phân phối ấy là một hàm phụ thuộc vào $\mathbf{w}$, thì khi đó, gọi $p(\mathcal{D} \mid \mathbf{w})$ là hàm likelihood (likelihood function).
Thay vì viết $p(\mathcal{D} \mid \mathbf{w})$ để dễ bị nhầm lẫn giữa phân phối xác suất và hàm likelihood, ta sẽ kí hiệu: \[ \mathcal{L}(\mathbf{w} \mid \mathcal{D}) = p(\mathcal{D} \mid \mathbf{w}) \] trong đó $\mathcal{L}(\mathbf{w} \mid \mathcal{D})$ là hàm likelihood có biến là $\mathbf{w}$ và không phải là một phân phối xác suất (why ?). Còn $p(\mathcal{D} \mid \mathbf{w})$ là phân phối xác suất có biến là $\mathcal{D}$.
Dựa vào định nghĩa của likelihood, ta có thể viết lại định lý Bayes như sau:
\[\text{posterior} \propto \text{likelihood} \times \text{prior}\]trong đó $\text{likelihood}, \text{posterior}$ và $\text{prior}$ đều là các hàm phụ thuộc vào $\mathbf{w}$. Còn giá trị $p(\mathcal{D})$ dưới mẫu là một hằng số, dùng để đảm bảo rằng phân phối hậu nghiệm ở bên phải định lý Bayes đúng là một phân phối (mật độ xác suất). Thông thường, $p(\mathcal{D})$ có thể được tính thông qua sum rule.
Áp dụng sum rule và product rule (Probability Densities) cho biến liên tục, ta có:
\[p(\mathcal{D}) = \int p(\mathcal{D} \mid \mathbf{w}) p(\mathbf{w}) d\mathbf{w}\]Vậy:
\[\begin{aligned} \int_{-\infty}^{\infty} p(\mathbf{w} \mid \mathcal{D}) d\mathbf{w} &= \int_{-\infty}^{\infty} \frac{p(\mathcal{D} \mid \mathbf{w})p(\mathbf{w})}{p(\mathcal{D})} d\mathbf{w} \\ &= \frac{\int p(\mathcal{D}\mid \mathbf{w})p(\mathbf{w}) d\mathbf{w}}{\int p(\mathcal{D}\mid \mathbf{w})p(\mathbf{w}) d\mathbf{w}} = 1 \end{aligned}\]Còn việc $p(\mathbf{w} \mid \mathcal{D}) \geq 0$ mình nghĩ khá là dễ thấy rồi. Nhờ $p(\mathcal{D})$ mà $p(\mathbf{w} \mid \mathcal{D})$ là một phân phối xác suất, ta còn có thể xem $p(\mathcal{D})$ như là một hằng số dùng để chuẩn hoá $p(\mathbf{w} \mid \mathcal{D})$.
Kí hiệu $\propto$ nghĩa là tỉ lệ. Ví dụ, chiều cao ($h$) $= 1.2 \times$ cân nặng ($w$), lúc này ta nói chiều cao tỉ lệ với cân nặng hay $h \propto w$. Ở định lý Bayes, nếu ta xem $1 / p(\mathcal{D})$ là một hằng số (mà nó là một hằng số thật, bởi vì $\mathcal{D}$ không đổi rồi) thì $p(\mathbf{w} \mid \mathcal{D}) \propto \mathcal{L}(\mathbf{w} \mid \mathcal{D})p(\mathbf{w})$.
Vậy sinh ra cái Bayes này làm gì, mục đích của chúng ta đó là cố gắng tìm bộ tham số $\mathbf{w}$ sao cho $p(\mathbf{w} \mid \mathcal{D})$ là tốt nhất, kiểu như ta đã biết trước tập dữ liệu $\mathcal{D}$ (tức là ta đã biết trước kết quả rồi), ta cần tìm mô hình (tham số $\mathbf{w}$) phù hợp với $\mathcal{D}$ nhất (tức là ta đi tìm nguyên nhân cho ra kết quả và nguyên nhân đó phải là phù hợp với kết quả nhất, vậy là tìm xác suất $p(\mathbf{w}\mid \mathcal{D})$ lớn nhất) (mình copy cách giải thích này từ
Trước khi quan sát được dữ liệu $\mathcal{D}$, ta tin rằng $\mathbf{w}$ sẽ tốt (là một mô hình phù hợp với $\mathcal{D}$) ở một mức độ nào đó, tức là $p(\mathbf{w})$, sau khi quan sát được dữ liệu ${} \mathcal{D}$ rồi, niềm tin về độ phù hợp của $\mathbf{w}$ với ${} \mathcal{D} {}$ sẽ thay đổi và có giá trị là $p(\mathbf{w} \mid \mathcal{D})$. Còn giá trị likelihood $p(\mathcal{D} \mid \mathbf{w})$ có thể được hiểu như sau: nếu giả sử tham số là $\mathcal{w}$ thì xác suất (hay mức độ niềm tin) mà dữ liệu ta quan sát được là $\mathcal{D}$.
Đối với frequentist thì ta sẽ dùng phương pháp maximum likelihood (MLE) để tìm giá trị $p(\mathcal{D} \mid \mathbf{w})$ lớn nhất từ đó tìm được $p(\mathbf{w} \mid \mathcal{D})$ lớn nhất (frequentist giả sử rằng $p(\mathbf{w})$ và $p(\mathcal{D})$ là các hằng số, ở góc nhìn của frequentist, ta sẽ xem $\mathbf{w}$ như là một giá trị mà ta ước lượng được, do đó $p(\mathbf{w})$ là một hằng số) Ta sẽ tìm hiểu phương pháp này ở phần Gaussian Distribution.
Còn đối với bayesian, ta có phương pháp gọi là maximum a posteriori estimation (MAP). Bayesian cho rằng $\mathbf{w}$ là một biến ngẫu nhiên chứ không phải một giá trị, do đó $p(\mathbf{w})$ là một phân phối. Vậy để tìm được $p(\mathbf{w} \mid \mathcal{D})$ lớn nhất ta phải tìm cả likelihood $p(\mathcal{D} \mid \mathbf{w})$ và prior $\mathcal{p}(\mathbf{w})$.