Exercises (Part I)
PRML Chapter 1 Exercises ( | Exercises (Part II))
Bài 1-1
Phương trình (1.1) như sau:
\[y(x, \mathbf{w}) = \sum_{j=0}^M x^j w_{j}\]Phương trình (1.2) như sau:
\[E(\mathbf{w}) = \frac{1}{2} \sum_{n=1}^N \left\{ y(x_{n}, \mathbf{w}) - t_{n} \right\}^2\]với $(x_1, \dots, x_{n})$ là các dữ liệu, $(t_{1}, \dots, t_{n})$ là các nhãn (hay là target) và $\mathbf{w}$ là bộ tham số. Để cực tiểu được hàm lỗi $E(\mathbf{w})$, ta chỉ cần tìm giá trị $\hat{\mathbf{w}}$, sao cho:
\[\nabla E(\hat{\mathbf{w}}) = \mathbf{0}\]với $\mathbf{0}$ là vector $0$. Do $\nabla E(\mathbf{w})$ là một vector nên để vector bằng $0$ thì từng phần tử bằng $0$, vậy ta cần tìm $\hat{w}_{i}$ sao cho:
\[\frac{\partial{E(\hat{\mathbf{w}})}}{\partial w_{i}} = 0\]Giờ bắt đầu biến đổi để tìm được $\hat{w}_i$ thôi nào. Ta có:
\[\begin{aligned} \frac{\partial{E(\hat{\mathbf{w}})}}{\partial w_{i}} &= \frac{1}{2} \sum_{n=1}^N \frac{\partial \{y(x_{n}, \mathbf{w}) - t_{n}\}^2}{\partial w_{i}} \\ &= \frac{1}{2} \sum_{n=1}^N \left[ \frac{\partial y(x_{n}, \mathbf{w})^2}{\partial w_{i}} - 2t_{n} \frac{\partial y(x_{n}, \mathbf{w})}{\partial w_{i}} + \frac{\partial t_{n}^2}{\partial w_{i}} \right] \\ &= \frac{1}{2} \sum_{n=1}^N \left[ 2y(x_{n}, \mathbf{w})\frac{\partial y(x_{n}, \mathbf{w})}{\partial w_{i}} - 2t_{n}x_{n}^i +0 \right] \\ &= \frac{1}{2} \sum_{n=1}^N [2y(x_{n}, \mathbf{w})x_{n}^i -2t_{n}x_{n}^i] \\ &= \sum_{n=1}^N \left[ \sum_{j=0}^M x_{n}^{i+j} w_{j} \right] - \sum_{n=1}^Nt_{n}x_{n}^i \end{aligned}\]Ở phương trình trên, tách phần trước dấu trừ, ta được:
\[\begin{aligned} \sum_{n=1}^N \left[ \sum_{j=0}^M x_{n}^{i+j} w_{j} \right] &= \sum_{n=1}^N (x_{n}^{i}w_{0} + \dots x_{n}^{i+M}w_{M}) \\ &= \sum_{n=1}^N x_{n}^iw_{0} + \dots + \sum_{n=1}^N x_{n}^{i+M}w_{M} \\ &= \sum_{j=0}^M \left( \sum_{n=1}^N x_{n}^{i+j} \right) w_{j} \end{aligned}\]Thay vào lại phương trình chỗ ta có:
\[\begin{aligned} \frac{\partial{E(\hat{\mathbf{w}})}}{\partial w_{i}} &= \sum_{n=1}^N \left[ \sum_{j=0}^M x_{n}^{i+j} w_{j} \right] - \sum_{n=1}^Nt_{n}x_{n}^i \\ &= \sum_{j=0}^M \left( \sum_{n=1}^N x_{n}^{i+j} \right) w_{j} - \sum_{n=1}^N t_{n}x_{n}^i \end{aligned}\]Đặt $\sum_{n=1}^N x_{n}^{i+j} = A_{ij}$ và $\sum_{n=1}^Nt_{n}x_{n}^i = T_{i}$. Khi đó:
\[\begin{aligned} \frac{\partial E(\mathbf{w})}{\partial w_{i}} &= 0 \\ \Leftrightarrow \sum_{j=0}^M A_{ij}w_{j} &= T_{i} \end{aligned}\]Vậy giá trị $\hat{w}_i$ cần tìm chính là nghiệm của phương trình trên.
Bài 1-2
Phương trình (1.122) là phương trình nghiệm $\hat{w}_i$ ở bài 1.1. Còn phương trình (1.4) như sau:
\[\tilde{E}(\mathbf{w}) = \frac{1}{2} \sum_{n=1}^N \{y(x_{n}, \mathbf{w}) - t_{n}\}^2 + \frac{\lambda}{2}||\mathbf{w||^2}\]trong đó $|\mathbf{w}|$ được gọi là chuẩn của vector $\mathbf{w}$ và có công thức là:
\[\|\mathbf{w}\| = \sqrt{ w_{0}^2 + \dots + w_{M}^2 }\]Ta có:
\[\begin{aligned} \frac{\partial{E(\hat{\mathbf{w}})}}{\partial w_{i}} &= \frac{1}{2} \sum_{n=1}^N \frac{\partial \left( \{y(x_{n}, \mathbf{w}) - t_{n}\}^2 \right)}{\partial w_{i}} + \frac{\lambda}{2}\dfrac{\partial ||\mathbf{w}||^2}{\partial w_{i}} \\ &= \frac{1}{2} \sum_{n=1}^N \left[ \frac{\partial y(x_{n}, \mathbf{w})^2}{\partial w_{i}} - 2t_{n} \frac{\partial y(x_{n}, \mathbf{w})}{\partial w_{i}} + \frac{\partial t_{n}^2}{\partial w_{i}} \right] + \frac{\lambda}{2} \frac{\partial||\mathbf{w}||^2}{\partial w_{i}} \\ &= \sum_{j=0}^M A_{ij}w_{j} -T_{i} + \lambda w_{i} \\ &= \sum_{j=0}^M A_{ij}w_{j} -T_{i} + \lambda w_{i} \\ \end{aligned}\]Vậy giá trị $\hat{w}_i$ chính là nghiệm của phương trình:
\[\sum_{j=0}^M A_{ij}w_{j} + \lambda w_{i} = T_{i}\]Bài 1-3
Bài này giải khá tương tự bài trong phần Probability Theory. Mình đặt biến ngẫu nhiên $B$ đại diện cho các hộp màu, biến ngẫu nhiên $F$ đại diện cho trái cây, $F= a$ là trái táo (apple), $F = o$ là trái cam (orange) và $F = l$ là trái chanh (lime). Ta có:
\[\begin{aligned} p(B = r) &= 0.2 \\ p(B = b) &= 0.2 \\ p(B = g) &= 0.6 \end{aligned}\]Tiếp theo, ta có xác suất chọn được trái táo khi đã chọn được một hộp màu lần lượt là:
\[\begin{aligned} p(F = a \mid B = r) &= \frac{3}{10} = 0.3 \\ p(F = a \mid B = b) &= \frac{1}{2} = 0.5 \\ p(F = a \mid B = g) &= \frac{3}{10} = 0.3 \end{aligned}\]Dùng sum rule, ta lại có:
\[\begin{aligned} p(F = a) &= \sum_{B} p(F=a, B) \\ &= \sum_{B} p(F=a \mid B)p(B) \\ &= p(F=a \mid B = r)p(B = r) + p(F=a \mid B=b)p(B=b) \\ &+ p(F=a \mid B=g)p(B = g) \\ &= 0.3 \times 0.2 + 0.5 \times 0.2 + 0.3 \times 0.6 \\ &= 0.34 \end{aligned}\]Vậy xác suất để chọn được một quả táo là $0.34$. Để tìm xác suất hộp ta chọn là hộp xanh lá $g$ khi đã chọn được quả táo, ta tìm xác suất $p(B = g \mid F = a)$ bằng cách dùng định lý Bayes:
\[p(B = g \mid F= a) = \frac{p(F=a \mid B=g)p(B =g)}{p(F=a)} = \frac{0.3 \times 0.6}{0.34} \approx 0.52\]Bài 1-4
WARNING: Bài này khá hardcore 💀
Giả sử ta có hàm khả vi $f(x)$ với $x$ là số thực (không phải biến ngẫu nhiên), để tìm giá trị lớn nhất của $f(x)$, ta đạo hàm $f’(x)$ sau đó cho $f’(x) = 0$ để tìm được giá trị $x$ thoả mãn, gọi là $\hat{x}$ đi. Tiếp theo, ta có một biến mới là $y$ với $x = g(y)$. Đổi biến hàm $f(x)$ sang $f(g(y))$ (là một hàm của $y$), ta đặt $\tilde{f}(y) = f(g(y))$ (để biết đây là một hàm của $y$). Để tìm giá trị lớn nhất của $\tilde{f}(y)$, ta đạo hàm và sau đó cho bằng $0$. Đầu tiên đạo hàm: \[ \begin{aligned} \frac{d\tilde{f}(y)}{dy} &= \frac{df(g(y))}{g(y)} \frac{dg(y)}{y}
\implies \tilde{f}’(y) = f’(g(y))g’(y) \end{aligned} \] Sau đó cho bằng $0$ (gọi giá trị làm đạo hàm bằng $0$ là $\hat{y}$): \[ \tilde{f}’(\hat{y}) = 0 \implies f’(g(\hat{y})) = 0 \hspace{3pt} \text{hoặc} \hspace{3pt} g’(\hat{y}) = 0 \hspace{3pt} \text{hoặc cả 2 $=0$} \] Xét trường hợp $f’(g(\hat{y})) = 0$, ta thấy rằng $f’(\hat{x}) = 0$, do đó $f’(g(\hat{y})) = f’(\hat{x}) \implies g(\hat{y}) = \hat{x}$. Vậy có nghĩa là ta có thể tìm giá trị lớn nhất của $f(x)$ thông qua $y$ với $x = g(y)$. Tương tự với trường hợp $f’(g(\hat{y})) = 0$ và $g’(\hat{y}) = 0$.
Note: Tuy nhiên ta cần để ý trường hợp chỉ $g’(\hat{y}) = 0$. Trong solution tác giả giả sử luôn $g’(\hat{y}) = 0$ bởi vì ta chỉ quan tâm đến trường hợp $f’(g(\hat{y})) = 0$ thôi, việc $g’(\hat{y}) = 0$ mà $f’(g(\hat{y})) \neq 0$ có thể được giải quyết bằng cách chọn một biến khác, gọi là $t$ đi, lúc này $x = \tilde{g}(t)$ và ta được $f’(\tilde{g}(\hat{t})) = 0$ và ta không cần quan tâm $\tilde{g}’(\hat{t})$ bằng $0$ hay khác $0$ nữa. Do mục đích là tìm giá trị lớn nhất của $f(x)$ thông qua một biến mới nào đó, do đó ta có thể chọn lại biến mới sao cho thoả mãn các giả sử của ta là được. Vậy ở đây, tác giả muốn nói là, với $x$ và $y$ (liên quan với nhau thông qua $x = g(y)$) không là biến ngẫu nhiên thì ta có thể tìm giá trị lớn nhất của $f(x)$ thông qua $y$. Nhưng đối với hai biến ngẫu nhiên $X$ và $Y$ thì việc này không xảy ra (không thể tìm giá trị lớn $f(X)$ thông $Y$) do bị ảnh hưởng bởi jacobian factor
Giờ xét $X$ và $Y$ là hai biến ngẫu nhiên với $X = g(Y$) (lưu ý $g$ là hàm khả nghịch). Đặt $p_x$ và $p_y$ lần lượt là hàm mật độ xác suất của $X$ và $Y$. Để tìm được mật độ xác suất của $Y$, ta dùng công thức 1.17 như sau:
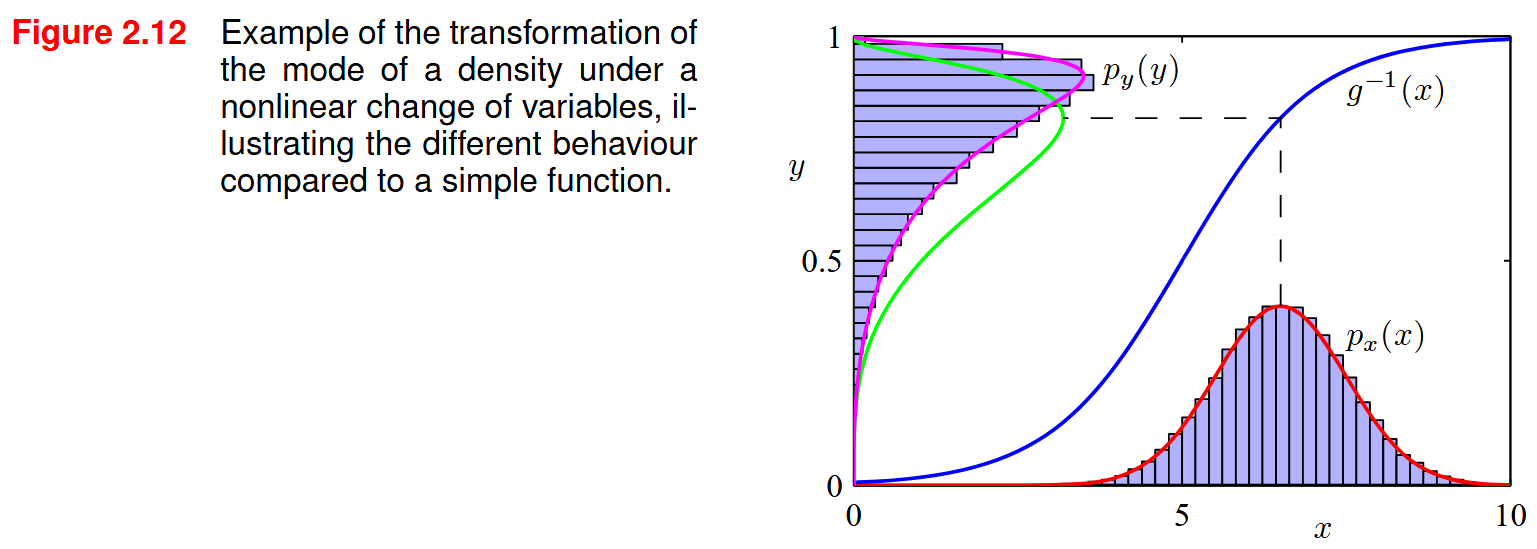
\[p_{y}(y) = p_{x}(g(y)) \hspace{2pt} \left|g'(y)\right|\]Giả sử giá trị $\hat{x}$ là giá trị để làm cho $p_x$ lớn nhất, tức là $p_{x}’(\hat{x}) = 0$. Để tìm giá trị lớn nhất của $p_y(y)$ ta đạo hàm và sau đó cho giá trị đạo hàm bằng $0$. Giả sử $g’(y) \neq 0$ (khi đó ta mới có thể đạo hàm $\lvert g’(y)\rvert$) và đặt $\lvert g’(y) \rvert= sg’(y)$ với $s \in {-1, 1}$.
Đầu tiên ta lấy đạo hàm:
\[\begin{aligned} p_{y}'(y) = \frac{dp_{y}(y)}{dy} &= \frac{dp_{x}(g(y))}{dy} sg'(y) + p_{x}(g(y)) \frac{dsg'(y)}{dy} \\ &= sp_{x}'(g(y))g'(y)\hspace{1pt}|g'(y)| + p_{x}(g(y))\hspace{1pt}sg''(y) \\ &= sp_{x}'(g(y))[g'(y)]^2 + sp_{x}(g(y))\hspace{1pt}g''(y) \\ \end{aligned}\]Giả sử giá trị $\hat{y}$ là giá trị để làm cho $p_y$ lớn nhất và giả sử $\hat{x} = g(\hat{y})$, tức là $p’_x(\hat{x}) = p’_x(g(\hat{y})) = 0$ (tương tự như $x$ và $y$ không là biến ngẫu nhiên). Khi đó:
\[\begin{aligned} p_{y}'(\hat{y}) &= sp_{x}'(g(\hat{y}))[g'(\hat{y})]^2 + sp_{x}(g(\hat{y}))\hspace{1pt}g''(\hat{y}) \\ &= sp_{x}(g(\hat{y}))g''(\hat{y}) \neq 0 \end{aligned}\]Vậy rõ ràng nếu $\hat{y}$ là giá trị làm cho $p_y$ lớn nhất và $\hat{x} =g(\hat{y})$ thì điều này lại sai, do đó $\hat{x} \neq g(\hat{y})$. Tức là nếu $X$ và $Y$ là biến ngẫu nhiên thì không có quan hệ nào giữa $\hat{x}$ và $g(\hat{y})$, do đó ta không thể tìm giá trị $X$ làm cho $p_x$ lớn nhất bằng cách tìm giá trị $Y$ làm cho $p_y$ lớn nhất.
Tuy nhiên, nếu ta chọn $g(Y) = X$ sao cho $g$ là một hàm tuyến tính thì mọi chuyện sẽ khác. Giả sử $X = g(Y) = \alpha Y + \beta$. Khi đó:
\[p'_{y}(\hat{y}) = sp_{x}(g(\hat{y}))g''(\hat{y}) = 0\]Do nếu $g(y) = \alpha y + \beta$ thì $g”(y) = 0$ với mọi $y$.
Vậy $p_y’(\hat{y}) = 0 \implies p_x’(g(\hat{y})) = 0 \implies p_x’(\hat{x}) = p_{x}(g(\hat{y})) = 0 \implies \hat{x} = g(\hat{y})$. Ta có thể thấy bằng việc chọn $g$ là một hàm tuyến tính thì $\hat{x} = g(\hat{y})$, do đó việc chọn hàm $g$ để biến đổi từ $X$ sang $Y$ là rất quan trọng.
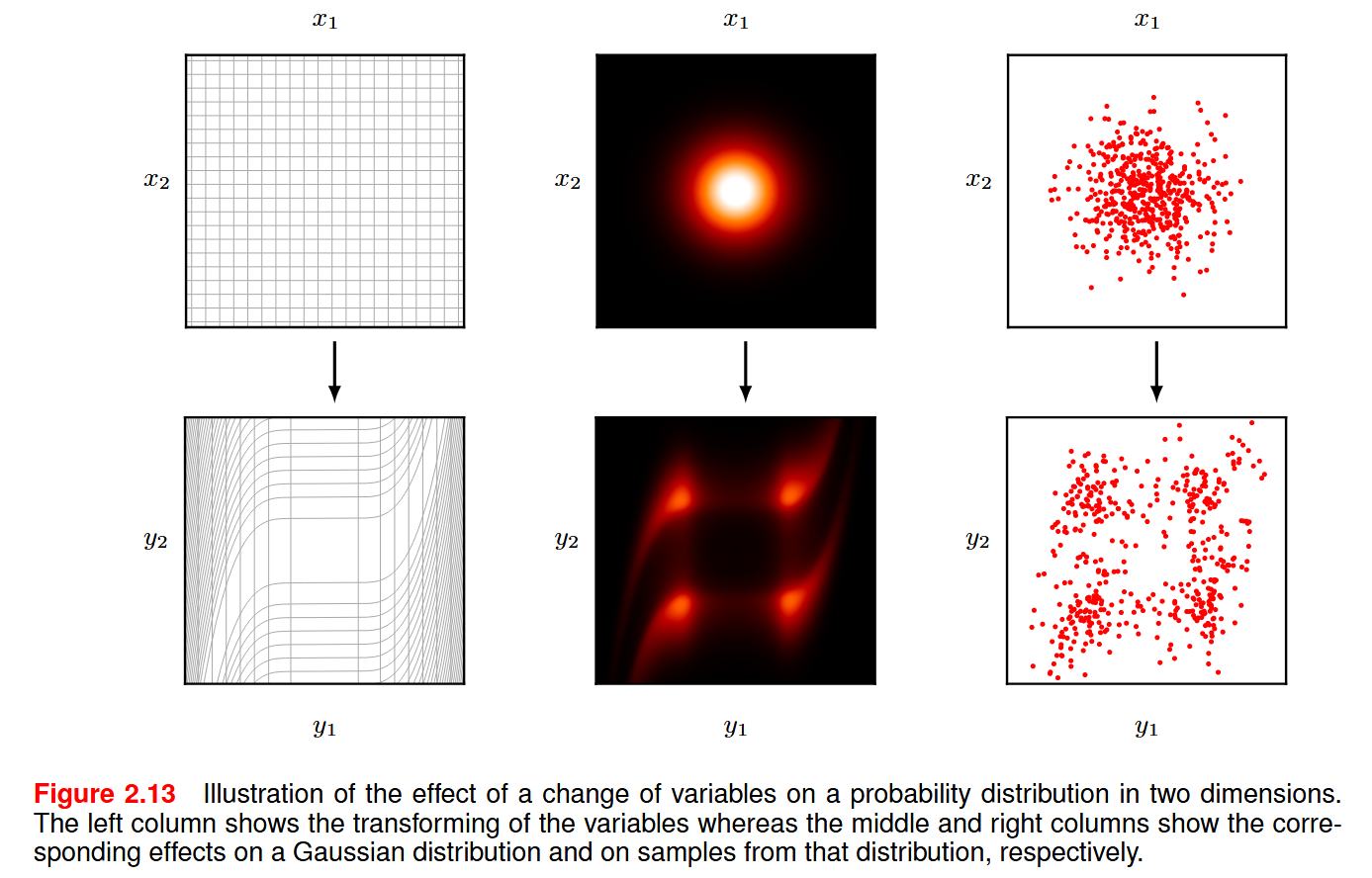
Trường hợp nhiều chiều
Công thức biến đổi pdf có thể áp dụng lên cho trường hợp vector ngẫu nhiên. Xét một pdf $p(\mathbf{x})$ trên một vector ngẫu nhiên $D$-chiều $\mathbf{x} = (x_{1}, \dots, x_{D})^T$, và giả sử ta biến đổi sang một vector ngẫu nhiên mới $\mathbf{y} =(y_{1}, \dots, y_{D})^T$ thông qua $\mathbf{x} = \mathbf{g}(\mathbf{y})$ ($\mathbf{g}$ là một hàm vector và ta giả sử $\mathbf{x}$ và $\mathbf{y}$ cùng chiều cho không phức tạp). Khi đó:
\[p_{\mathbf{y}}(\mathbf{y}) = p_{\mathbf{x}}(\mathbf{x}) | \det \mathbf{J}|\]trong đó $\mathbf{J}$ là jacobian matrix và:
\[\begin{aligned} \mathbf{J} &= \begin{bmatrix} \frac{\partial \mathbf{g}}{\partial y_{1}} & \dots & \frac{\partial \mathbf{g}}{\partial y_{D}} \end{bmatrix} \\ &= \begin{bmatrix} \nabla^T g_{1} \\ \vdots \\ \nabla^T g_{D} \end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial g_{1}}{\partial y_{1}} & \dots & \frac{\partial g_{1}}{\partial y_{D}} \\ \vdots & \ddots & \vdots \\ \frac{\partial g_{D}}{\partial y_{1}} & \dots & \frac{\partial g_{D}}{\partial y_{D}} \end{bmatrix} \end{aligned}\]Ta có thể tưởng tượng việc đổi biến là việc thay đổi đi “space” (kiểu như expanding hay contracting, …) của biến đó, ví dụ như một vùng vô cùng nhỏ (infinitesimal region) $\Delta \mathbf{x}$ xung quanh điểm $\mathbf{x}$ sẽ được biến đổi sang một vùng vô cùng nhỏ mới $\Delta \mathbf{y}$ xung quanh điểm $\mathbf{x} = \mathbf{g}(\mathbf{y})$ (vùng này có thể expand hoặc contract lại). Giá trị tuyệt đối của định thức của Jacobian biểu diễn tỉ lệ giữa các vùng này với nhau (tương tự trong 2D, $dx /dy$, các “vùng vô cùng nhỏ” này là “các đoạn vô cùng nhỏ”).
Bài 1-5
Dựa vào các tính chất sau của kì vọng
Khi đó:
\[\begin{aligned} \text{var}[f] &= \mathbb{E}[(f(X) - \mathbb{E}[f(X)])^2] \\ &= \mathbb{E}[f(X)^2 - 2f(X)\mathbb{E}[f(X)] + \mathbb{E}[f(X)]^2] \\ &= \mathbb{E}[f(X)^2] -2\mathbb{E}[f(X)\mathbb{E}[f(X)]] + \mathbb{E}[\mathbb{E}[f(X)]^2] \\ &= \mathbb{E}[f(X)^2] - 2\mathbb{E}[f(X)]\mathbb{E}[f(X)] + \mathbb{E}[f(X)]^2 \\ &= \mathbb{E}[f(X)^2] - \mathbb{E}[f(X)]^2 \end{aligned}\]Bài 1.7
Trước tiên có một cái mình cần làm rõ, ta có:
\[\begin{aligned} I^2 &= \left[ \int_{-\infty}^{\infty} \exp\left( -\frac{1}{2\sigma^2} x^2 \right) dx \right]^2 \\ &= \int_{-\infty}^{\infty}\exp\left( -\frac{1}{2\sigma^2} x^2 \right)dx\int_{-\infty}^{\infty}\exp\left( -\frac{1}{2\sigma^2} x^2 \right)dx \\ &= \int_{-\infty}^{\infty}\exp\left( -\frac{1}{2\sigma^2} x^2 \right)dx\int_{-\infty}^{\infty}\exp\left( -\frac{1}{2\sigma^2} y^2 \right)dy \\ &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \exp\left( -\frac{1}{2\sigma^2}x^2 - \frac{1}{2\sigma^2}y^2 \right) dx dy \end{aligned}\]Chuyển từ toạ độ $(x, y)$ sang toạ độ cực $(r, \theta)$ cho tích phân $I^2$ (tìm hiểu ở
Đặt $u = r^2$ ta có $\frac{1}{2}du = r dr$:
\[\begin{align*} I^{2} &= \int_{0}^{2\pi} \frac{1}{2} \left[ \int_{0}^{\infty} \exp\left( -\frac{1}{2\sigma^2} u \right) du \right] d \theta \end{align*}\]Xét tích phân của $u$, ta có:
\[\begin{align*} \int_{0}^{\infty} \exp\left( -\frac{1}{2\sigma^2} u \right) du &= \lim_{ n \to \infty } \int_{0}^{n} \exp\left( -\frac{1}{2\sigma^2} u \right) du\\ &= \lim_{ n \to \infty } \left[ \left. -2\sigma^2 \exp\left( -\frac{1}{2\sigma^2}u \right) \right|_{0}^n \hspace{3pt} \right] \\ &= \lim_{ n \to \infty } \left[ -2\sigma^2\exp\left( -\frac{1}{2\sigma^2}n \right) + 2\sigma^2 \right] \\ &= 2\sigma^2 \end{align*}\]Thay vào tích phân $I^2$, ta được:
\[\begin{align*} I^2 &= \int_{0}^{2\pi} \sigma^2 d\theta \\ &= \left. \sigma^2 \theta \right|_{0}^{2\pi} \\ &= 2\pi \sigma^2 \\ \implies I &= (2\pi \sigma^2)^{1/2} \end{align*}\]Vậy:
\[\int_{-\infty}^{\infty} \exp\left( -\frac{1}{2\sigma^2}x^2 \right)dx = (2\pi \sigma^2)^{1/2}\]Để áp dụng được tích phân này lên phân phối chuẩn $\mathcal{N}(\mu, \sigma^2)$, ta đặt $z = x - \mu$, khi đó $dz = dx$, vậy:
\[\begin{align*} \int_{-\infty}^{\infty} \mathcal{N}(x \mid \mu, \sigma^2) &= \int_{-\infty}^{\infty} \frac{1}{(2\pi \sigma^2)^{1/2}} \exp\left( -\frac{1}{2\sigma^2}(x - \mu)^2 \right) dx \\ &= \int_{-\infty}^{\infty} \frac{1}{(2\pi \sigma^2)^{1/2}} \exp\left( -\frac{1}{2\sigma^2} z^2 \right) dz \\ &= \frac{1}{(2\pi \sigma^2)^{1/2}} \int_{-\infty}^{\infty} \exp\left( -\frac{1}{2\sigma^2}z^2 \right) dz \\ &= 1 \end{align*}\]Bài 1-8
WARNING: Bài này khá hardcore đấy 💀
Nhắc lại: Kì vọng của phân phối chuẩn: \[ \mathbb{E}[X] = \int_{-\infty}^{\infty} \mathcal{N}(x \mid \mu, \sigma^2) x dx = \mu \] Moment bậc 2 của phân phối chuẩn: \[ \mathbb{E}[X^2] = \int_{-\infty}^{\infty} \mathcal{N}(x \mid \mu, \sigma^2) x^2 dx = \mu^2 + \sigma^2 \] Phương sai của phân phối chuẩn \[ \text{var}[X] = \sigma^2 \]
Đầu tiên, đặt $z = x- \mu \implies x = z + \mu$ vậy $dx = dz$. Thay $z$ vào tích phân của $\mathbb{E}[X]$, ta được:
\[\begin{align*} \mathbb{E}[X] &= \int_{-\infty}^{\infty} \frac{1}{(2\pi \sigma^2)^{1/2}} \exp\left( \frac{-1}{2\sigma^2}z^2 \right) (z + \mu) dz \\ &= \frac{1}{(2\pi \sigma^2)^{1/2}} \left[ \int_{-\infty}^{\infty} \exp\left( -\frac{1}{2\sigma^2}z^2 \right) z dz + \mu \int_{-\infty}^{\infty} \exp\left( -\frac{1}{2\sigma^2} z^2 \right) dz \right] \\ \end{align*}\]Xét tích phân phía bên trái dấu $+$ nằm trong ngoặc vuông, đặt:
\[f(z) = \exp\left( -\frac{1}{2\sigma^2} z^2 \right) z\]với mọi $z \in \mathbb{R}$, ta có:
\[\begin{align*} f(-z) &= \exp\left( -\frac{1}{2\sigma^2}(-z)^2 \right)(-z) \\ &= -\left[\exp\left( -\frac{1}{2\sigma^2}z^2 \right)z\right] \\ &= -f(z) \end{align*}\]do đó phần tích phân mà ta đang xét là tích phân của hàm lẻ
Vì vậy:
\[\int_{-\infty}^{\infty} \exp\left( \frac{-1}{2\sigma^2} z^2 \right)z dz = 0\]Còn phần tích phân phía sau dấu $+$ trong ngoặc vuông đã được ta chứng minh ở bài 1.7 phía trên và có giá trị là $(2\pi \sigma^2)^{1/2}$. Vậy ta có:
\[\begin{align*} \mathbb{E}[X] &= \frac{1}{(2\pi \sigma^2)^{1/2}} [0 + \mu (2\pi \sigma^2)^{1/2}] \\ &= \mu \end{align*}\]Đặt:
\[f(\sigma^2) = \int_{-\infty}^{\infty} \mathcal{N}(x \mid \mu, \sigma^2) dx\]Theo tích phân Leibniz
Giờ vấn đề là ta phải đạo hàm phân phối chuẩn theo $\sigma^2$, trước tiên, ta đặt:
\[\begin{align*} g(\sigma^2) &= \frac{1}{(2\pi \sigma^2)^{1/2}} \\ h(\sigma^2) &= \exp\left( -\frac{1}{2\sigma^2} (x-\mu)^2 \right) \\ \implies \mathcal{N}(x \mid \mu, \sigma^2) &= g(\sigma^2)h(\sigma^2) \\ \end{align*}\]Vậy:
\[\frac{\partial \mathcal{N}(x \mid \mu, \sigma^2)}{\partial \sigma^2} = \frac{\partial g(\sigma^2)}{\partial \sigma^2}h(\sigma^2) + g(\sigma^2) \frac{\partial h(\sigma^2)}{\partial \sigma^2}\]Để giải được phương trình trên, ta tìm từng đạo hàm, đầu tiên là $g(\sigma^2)$:
\[\begin{align*} \frac{\partial g(\sigma^2)}{\partial \sigma^2} &= \frac{1}{(2\pi)^{1/2}} \frac{\partial 1 / [(\sigma^2)^{1/2}]}{\partial \sigma^2} \\ &= \frac{1}{(2\pi)^{1/2}} \left( -\frac{1}{2} \frac{1}{(\sigma^2)^{3/2}} \right) \\ &= \frac{1}{(2\pi)^{1/2}} \left( -\frac{1}{2} \frac{1}{(\sigma^2)^{1/2}\sigma^2} \right) \\ &= -\frac{1}{2\sigma^2}g(\sigma^2) \end{align*}\]tiếp theo là $h(\sigma^2)$:
\[\begin{align*} \frac{\partial h(\sigma^2)}{\partial \sigma^2} &= -\frac{\partial 1/(2\sigma^2)}{\partial \sigma^2}[(x-\mu)^2 h(\sigma^2)] \\ &= \frac{1}{2} \frac{1}{\sigma^4} (x-\mu)^2 h(\sigma^2) \\\\ &= \frac{1}{2\sigma^2} \frac{(x-\mu)^2}{\sigma^2} h(\sigma^2) \end{align*}\]Kết hợp lại, ta được:
\[\begin{align*} \frac{\partial \mathcal{N}(x \mid \mu, \sigma^2)}{\partial \sigma^2} &= -\frac{1}{2\sigma^2}g(\sigma^2)h(\sigma^2) + \frac{1}{2\sigma^2} \frac{(x-\mu)^2}{\sigma^2} g(\sigma^2)h(\sigma^2) \\ &= \frac{1}{2\sigma^2}g(\sigma^2)h(\sigma^2) \left[\frac{(x-\mu)^2}{\sigma^2} - 1 \right] \\ &= \frac{1}{2\sigma^2}\left[ \frac{(x-\mu)^2}{\sigma^2} - 1 \right] \mathcal{N}(x \mid \mu, \sigma^2) \end{align*}\]Thực hiện đạo hàm 2 vế, ta có:
\[\begin{align*} &\frac{\partial f(\sigma^2)}{\partial \sigma^2} = \frac{\partial 1}{\partial \sigma^2} \\ &\Leftrightarrow \int_{-\infty}^{\infty} \frac{1}{2\sigma^2}\left[ \frac{(x-\mu)^2}{\sigma^2} - 1 \right] \mathcal{N}(x \mid \mu, \sigma^2) dx = 0 \\ &\Leftrightarrow \frac{1}{\sigma^2}\int_{-\infty}^{\infty} (x-\mu)^2 \mathcal{N}(x \mid \mu, \sigma^2) dx - \int_{-\infty}^{\infty} \mathcal{N}(x \mid \mu, \sigma^2) dx = 0 \\ &\Leftrightarrow \frac{1}{\sigma^2}\int_{-\infty}^{\infty} (x-\mu)^2 \mathcal{N}(x \mid \mu, \sigma^2) dx - 1 = 0 \\ &\Leftrightarrow \int_{-\infty}^{\infty} (x-\mu)^2 \mathcal{N}(x \mid \mu, \sigma^2) dx = \sigma^2 \\ &\Leftrightarrow \mathbb{E}[(X-\mu)^2] = \sigma^2 \\ &\Leftrightarrow \text{var}[X] = \sigma^2 \end{align*}\]Vậy ta chứng minh được phương sai của phân phối chuẩn là $\sigma^2$, tiếp theo:
\[\begin{align*} \text{var}[X] &= \mathbb{E}[X^2] - \mathbb{E}[X]^2 \\ \implies \mathbb{E}[X^2] &= var[X] + \mathbb{E}[X]^2 \\ &= \sigma^2 + \mu^2 \end{align*}\]Bài 1-9
Như đã chứng minh ở bài 1.4, khi mà ta đổi biến ngẫu nhiên $X$ có phân phối xác suất $f_{X}$ sang biến ngẫu nhiên $Y$ với $X = g(Y)$ và $g$ là hàm tuyến tính thì ta có thể tìm giá trị lớn nhất của $f_{X}$ thông qua $f_{Y}$. Ngoài ra ta có thể tìm $f_{Y}$ thông qua công thức sau:
\[f_{Y}(y) = f_{X}(g(y)) |g'(y)|\]Đặt $g(Y) = \sigma Y + \mu$ và $X \sim \mathcal{N}(\mu, \sigma^2)$, nên ta có:
\[\begin{align*} f_{X}(g(y)) &= \frac{1}{(2\pi\sigma^2)^{1/2}} \exp\left( -\frac{1}{2\sigma^2}[(\sigma y + \mu) - \mu]^2 \right) \\ &= \frac{1}{(2\pi \sigma^2)^{1/2}} \exp\left( -\frac{1}{2}y^2 \right) \\ \text{và} \hspace{5pt} g'(y) &= \sigma \end{align*}\]do đó:
\[\begin{align*} f_{Y}(y) &= \frac{1}{(2\pi \sigma^2)^{1/2}} \exp\left( -\frac{1}{2}y \right) |\sigma| \\ &= \frac{1}{(2\pi \sigma^2)^{1/2}} \exp\left( -\frac{1}{2}y^2 \right) \sigma \\ &= \frac{1}{(2\pi)^{1/2}} \exp\left( -\frac{1}{2}y^2 \right) \end{align*}\]Lấy đạo hàm bằng $0$, ta có:
\[\begin{align*} f_{Y}'(y) &=\frac{1}{(2\pi)^{1/2}} (-y) \exp\left( -\frac{1}{2}y^2 \right) \\ \implies f'_{Y}(y) &= 0 \\ \Leftrightarrow y &= 0 \\ \implies x &= \mu \end{align*}\]Để xác minh giá trị đạo hàm bằng $0$ là cực đại, ta có:
\[\begin{align*} f''_{Y}(y) &= \frac{1}{(2\pi)^{1/2}} \left[ -\exp\left( -\frac{1}{2}y^2 \right) + y^2 \exp\left( -\frac{1}{2}y^2 \right) \right] \\ &= \frac{1}{(2\pi)^{1/2}} \exp\left( -\frac{1}{2}y^2 \right) (y^2 - 1) \end{align*}\]tại $y = 0$, $f_{Y}”(y) < 0$ do đó $y = 0$ là điểm làm cho $f_{Y}(y)$ cực đại.
Vậy giá trị $x$ làm cho phân phối $f_{X}$ lớn nhất là $x = \mu$. Do đó $\mu$ chính là mode của phân phối chuẩn.
Bài 1-10
Khi hai biến ngẫu nhiên $X$ và $Z$ độc lập với nhau thì $p(x, z) = p_{x}(x)p_{z}(z)$ với $p(x, z)$ là mật độ xác suất đồng thời của $X$ và $Z$, còn $p_{x}$ và $p_{z}$ lần lượt là mật độ xác suất của $X$ và $Z$.
Ta có:
\[\begin{align*} \mathbb{E}[X + Z] &= \iint (x + z)p(x, z)dxdz \\ &= \iint (x+z)p_{x}(x)p_{z}(z)dxdz \\ &= \iint xp_{x}(x)p_{z}(z)dxdz + \iint zp_{x}(x)p_{z}(z)dxdz \\ &= \int p_{z}(z)\left[ \int xp_{x}(x)dx \right]dz + \int p_{x}(x)\left[ \int zp_{z}(z)dz \right]dx \\ &= \mathbb{E}[X] \int p_{z}(z)dz + \mathbb{E}[Z] \int p_{x}(x)dx \\ &= \mathbb{E}[X] + \mathbb{E}[Z] \end{align*}\]Do $p_{x}$ là một hàm mật độ xác suất nên: \[ \int_{-\infty}^{\infty} p_{x}(x) dx = 1 \] tương tự với $p_{z}$.
Ta có:
\[\text{var}[X + Z] = \mathbb{E}[(X+Z)^2] - (\mathbb{E}[X+Z])^2 \\\]Bây giờ, ta sẽ phân tích $\mathbb{E}[(X +Z)^2]$ thử:
\[\begin{align*} &\mathbb{E}[(X+Z)^2] = \iint (x+z)^2 p(x, z)dxdz \\ &= \iint (x^2 + 2xz + z^2) p(x, z)dxdz \\ &= \iint x^2p_{x}(x)p_{z}(z)dxdz + 2\iint xzp_{x}(x)p_{z}(z)dxdz + \iint z^2p_{x}(x)p_{z}(z)dxdz \\ &= \int p_{z}(z) \left[ \int x^2 p_{x}(x)dx \right]dz + \int p_{x}(x) \left[ \int z^2 p_{z}(z)dz \right]dx + 2\int xp_{x}(x)dx \int zp_{z}(z)dz \\ &= \mathbb{E}[X^2] + \mathbb{E}[Z^2] + 2\mathbb{E}[X] \mathbb{E}[Z] \end{align*}\]Thay vào phương trình $\text{var}[X + Z]$, ta có:
\[\begin{align*} \text{var}[X + Z] &= \mathbb{E}[X^2] + \mathbb{E}[Z^2] + 2\mathbb{E}[X]\mathbb{E}[Z] - (\mathbb{E}[X] + \mathbb{E}[Z])^2 \\ &= (\mathbb{E}[X^2] - \mathbb{E}[X]^2) + (\mathbb{E}[Z^2] - \mathbb{E}[Z]^2) \\ &= \text{var}[X] + \text{var}[Z] \end{align*}\]